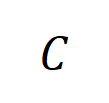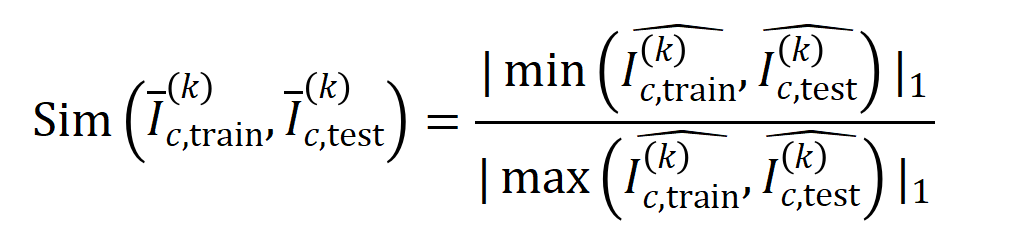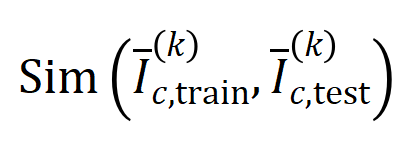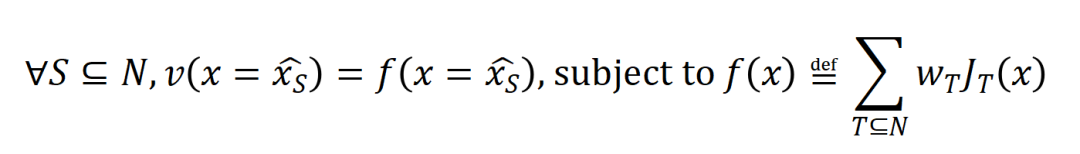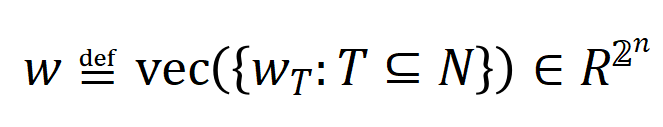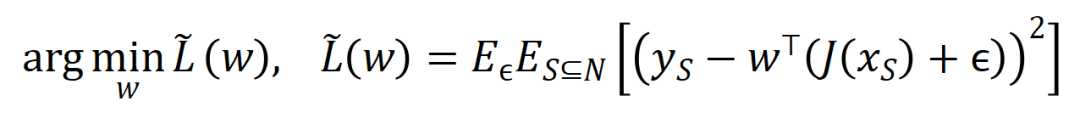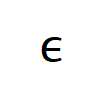AIxiv专栏是机器之心发布学术、技能内容的栏目。往时数年,机器之心AIxiv专栏吸收报谈了2000多篇内容,掩盖全球各大高校与企业的顶级实验室,有用促进了学术交流与传播。要是您有优秀的使命想要共享,接待投稿或者联系报谈。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com
本文作家为张俊鹏、任启涵、张拳石,其中张俊鹏是张拳石老诚的准入学博士生,任启涵是张拳石老诚的博士生。
本文领先简单总结了『等效交互可解释性表面体系』(20 篇 CCF-A 及 ICLR 论文),并在此基础上,严格推导并瞻望出神经相聚在覆按历程中其主张表征过火泛化性的能源学变化,即在某种进程上,咱们不错解释在覆按历程中神经相聚在职意时候点的泛化性过火内在根因。
一、弁言
永恒以来,咱们团队一直在想考可解释性领域的一个终极问题,即什么才是解释性领域的第一性旨趣?所谓第一性旨趣,目下莫得一个被迢遥承袭的框架,世上本无路,咱们需要渐渐去界说这么一个路。咱们需要在一个新的表面体系中,提议无数的公感性要求,得出一个不错从不同的角度全场地精准严谨解释神经相聚内在机理的表面。一套表面系统能严谨解释神经相聚的方方面面才叫 “第一性旨趣”。
要是你的确在严谨地作念 “科学”,那么第一性旨趣一定不是瞎想中简单,而是一个复杂的体系,需要究诘护理到深度学习中方方面面纷纭复杂的欢喜。天然,要是你主不雅上不肯意或者不信一个表面需要饱和严谨,那么究诘会变得简单千万倍。就像物理学的圭表模子一定比牛顿定律复杂,取决于你但愿走哪条路。
沿着这个场地,咱们团队孤独重新构建了『等效交互可解释性表面体系』,并基于此表面,从三个角度来解释神经相聚的内在机理。
1. 语义解释的表面基础:数学讲明神经相聚的有筹商逻辑是否不错被极少秀气化逻辑所充分掩盖(充认识释)。『讲明神经相聚的有筹商逻辑是否不错被有限秀气化逻辑解释自大』这一命题是解释神经相聚的根蒂命题。要是此命题被证伪,则从根蒂上讲,神经相聚的可解释性将是衰颓的,整个的解释性算法只可提供近似的解读,而无法精准地掩盖整个的有筹商逻辑。运气的是,咱们找到了在大部分愚弄中神经相聚都不错知足的面向荫庇鲁棒性的三个常见的条款,况且数学讲明了知足这三个条款的神经相聚的有筹商逻辑不错被写成秀气化的交互主张。
参见 https://zhuanlan.zhihu.com/p/693747946
2. 寻找性能贪图背后的可讲明、可考据的根因:将神经相聚泛化性和鲁棒性等终极性能贪图的根因拆分具体少数细节逻辑。对神经相聚性能(鲁棒性、泛化性)的解释是神经相聚可解释性领域的另一个首要问题。关联词,目下东谈主们普遍以为神经相聚性能是对神经相聚举座的形容,而神经相聚无法像东谈主类一样将我方的分类判断拆解成具象化的、极少的有筹商逻辑。在这方面,咱们给出了不一样的不雅点 —— 将性能贪图与具象化的交互之间缔造起数学关系。咱们讲明了 1. 等效交互的复杂度不错径直决定神经相聚的抗争鲁棒性 / 挪动性,2. 交互的复杂度决定了神经相聚的表征才调,3. 并解释神经相聚的泛化才调 [1],和 4. 解释神经相聚的表征瓶颈。
参见1:https://zhuanlan.zhihu.com/p/369883667
参见2:https://zhuanlan.zhihu.com/p/361686461
参见3:https://zhuanlan.zhihu.com/p/704760363
参见4:https://zhuanlan.zhihu.com/p/468569001
3. 和洽工程性深度学习算法。由于穷乏基础表面的支捏,目下深度学习算法大都是陶冶性的、工程性的。可解释性领域的第一性旨趣应该不错承担起将前东谈主的无数工程性陶冶总结为科学法规的任务。在等效交互可解释性表面体系下,咱们团队既讲明了 14 种不同的输入伏击性归因算法的经营本色在数学上都不错和洽写成对交互作用的再分拨花样。此外,咱们还和洽了 12 种进步抗争挪动性的算法,讲明了整个进步抗争挪动性算法的一个各人机理是裁汰抗争扰动之间的交互服从,完毕了对神经相聚可解释性场地大部单干程性算法的表面凝练。
参见1:https://zhuanlan.zhihu.com/p/610774894
参见2:https://zhuanlan.zhihu.com/p/546433296
在等效交互可解释性表面体系下,咱们的团队在之前的究诘中也曾告成发表了 20 篇 CCF-A 类和机器学习顶级会议 ICLR 论文,咱们也曾从表面和实验上充认识答了上述问题。
二、本文究诘空洞
沿着上述表面框架,在这篇知乎著作中,咱们但愿精准解释出神经相聚覆按历程中泛化性的变化法规,具体地触及两篇论文。
1.Junpeng Zhang, Qing Li, Liang Lin, Quanshi Zhang,“Two-Phase Dynamics of Interactions Explains the Starting Point of a DNN Learning Over-Fitted Features”,in arXiv: 2405.10262
2.Qihan Ren, Yang Xu, Junpeng Zhang, Yue Xin, Dongrui Liu, Quanshi Zhang,“Towards the Dynamics of a DNN Learning Symbolic Interactions” in arXiv:2407.19198

图 1:两阶段欢喜的暗示图。在第一阶段,神经相聚渐渐根除中高阶交互,学习低阶交互;在第二阶段,神经相聚渐渐建模阶数无间增大的交互。当神经相聚覆按历程中测试损结怨覆按亏空之间的 loss gap 动手增大时,神经相聚恰好也投入覆按的第二阶段。
咱们但愿在等效交互框架里提议新的表面,精准瞻望出神经相聚每一个时候点上神经相聚所学到的交互主张的数目、复杂度,以及泛化性变化的能源学法规(如图 1 所示)。具体地,咱们但愿讲明出两方面论断。
第一,基于前东谈主的讲明(一个神经相聚的有筹商逻辑不错被严格解构线路为几十个交互主张服从的和的花样),进一步严格推导出在整个这个词覆按历程中,神经相聚所建模的交互服从的变化能源学历程 —— 即表面需精准瞻望出在不同覆按阶段,神经相聚所建模的交互主张的散布的变化 —— 推导出哪些交互会在哪个时候点上被学习到。
第二,寻找充分的字据,讲明所推导的交互复杂度的变化法规客不雅反馈出神经相聚在全覆按周期中泛化性变化的法规。
综上两点,咱们但愿具体澈底解释自大神经相聚的泛化性变化的内在根因。
与前东谈主的关系:天然巨匠可能第一反应意想神经正切核(NTK)[2],然则神经正切核仅仅把参数的变化弧线解了出来,而没办法进一步真切到有筹商逻辑层面进行解释,莫得将神经相聚建模的主张表征与其泛化性的关系缔造起来,对泛化性的分析依然停留在特征空间分析的层面,而莫得在【秀气化主张逻辑】与【泛化性】之间缔造起严格的关系。
三、两大究诘布景
污蔑 1:神经相聚的第一性表征是『等效交互』,而不是神经相聚的参数和结构。单纯从结构层面分析神经相聚是东谈主们对神经相聚泛化根蒂表征的误解。目下大部分心经相聚泛化性究诘主要着眼于神经相聚的结构、特征、以及数据。东谈主们以为不同的神经相聚结构就天然对应不同的函数,并天然展现出不同的性能。
然则,事实上,如图 2 所示,结构的区别仅仅神经相聚表征的名义花样。裁撤有明显弱势的对性能有明显影响的神经相聚,整个其他不错完毕 SOTA 性能的具有不同结构的神经相聚经常都建模了相似的等效交互表征,即不同结构的高性能神经相聚在等效交互表征上经常都是同归殊途的 [3, 4]。诚然神经相聚其中层特征里面是复杂的参差词语的,诚然不同神经相聚所建模的特征向量大相径庭,诚然神经汇注首单个神经元经常建模了相对比较参差词语的语义(不是严格自大的语义),然则神经相聚作为一个举座,咱们从表面上讲明神经相聚的所建模的交互关系是稀疏的秀气化的(而不是特征的稀疏性,具体见 “四、交互的界说” 章节),而且面向换取任务的实足不同的神经相聚经常建模了相似的交互关系。
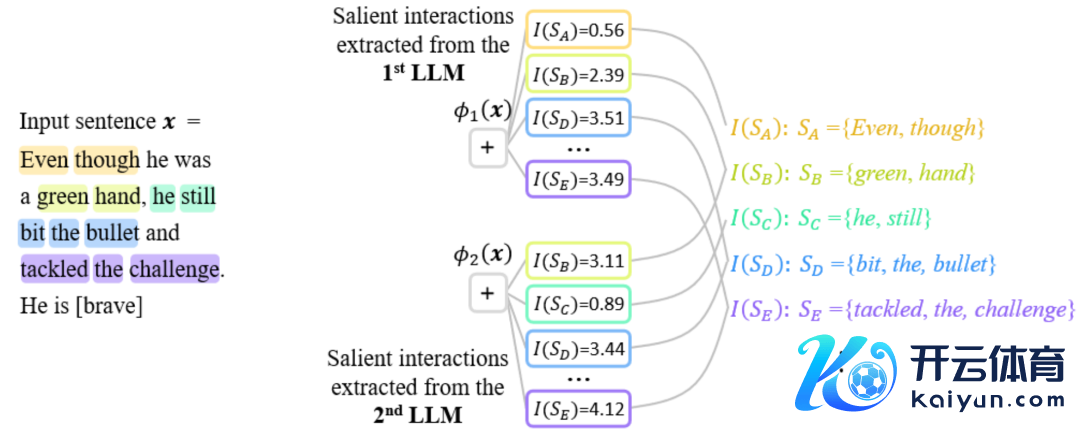
图 2:不同结构的神经相聚所建模的等效交互经常是同归殊途的。关于一个换取的输入句子,面向两个换取任务的两个实足不同的神经相聚建模经常相似的交互。
由于不同神经相聚的参数和覆按样本不一样,两个神经汇注首莫得任何一个神经元在表征上具有严格的逐个双应关系,且每一个神经元经常建模着不同语义的羼杂模式。比拟之下,正如上段分析,神经相聚所建模的交互表征执行上是不同神经相聚表征中的不变量。因此,咱们有事理以为神经相聚根蒂表征是等效交互,而不是其载体(参数和覆按样本),秀气化交互表征可能代表了常识表征的第一性旨趣(被交互的稀疏性定理、无尽拟合性定理、以及同归殊途欢喜所保证,见 “四、交互的界说” 章节,具体详备究诘见底下知乎著作。
参见:https://zhuanlan.zhihu.com/p/633531725
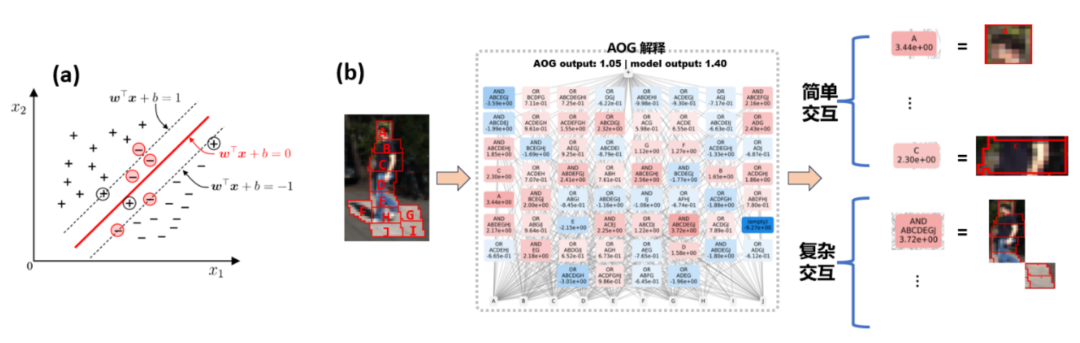
污蔑 2:神经相聚的泛化性问题是一个羼杂模子问题,而不是一个高维空间的向量。如图 3 所示,传统的泛化性分析老是假定单个样本举座是高维空间的一个点,执行上神经相聚对单个样本的表征是 mixture model 的花样 —— 执行上通过无数不同的交互来抒发。咱们发现简单交互的泛化才调比复杂交互的泛化才调更强,是以不再安妥用一个简单标量来蒙眬线路整个这个词神经相聚在不相通本上的泛化才调。违反,合并个神经相聚在不同的样本上建模了不同复杂度的交互关系,而不同复杂度的交互经常对应着不同泛化才调。迢遥情况下,神经相聚建模的高阶(复杂)的交互经常难以泛化到测试样本上(测试样本上不会触发换取的交互),代表过拟合表征,而神经相聚建模的低阶(简单)交互经常代表泛化性较强的表征,具体详备究诘见 [1]。
图 3:(a)传统的泛化性分析老是假定单个样本举座是高维空间的一个点。(b)执行上神经相聚对单个样本的表征是 mixture model 的花样,神经相聚在单个样本会建模简单交互(可泛化的交互)和复杂交互(不行泛化的交互)。
四、交互的界说
让咱们磋商一个深度神经相聚 和一个输入样本 ,它包含 个输入变量,咱们用集中 线路这些输入变量的全集。令 线路 DNN 在样本 上的一个标量输出。关于一个面向分类任务的神经相聚,咱们不错从不同角度来界说其标量输出。举例,关于多类别分类问题, 不错界说为 ,也不错界说为 softmax 层之前该样本实在标签所对应的标量输出。这里, 线路实在标签的分类概率。这么,针对每个子集 ,咱们不错用底下公式来界说 中整个输入变量之间 “等效与交互” 和 “等效或交互”。
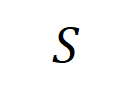
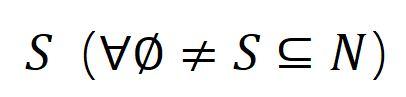
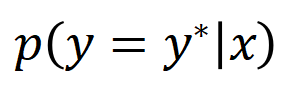

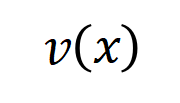
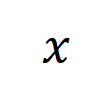
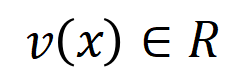
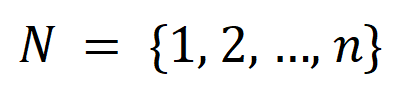
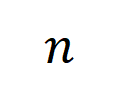
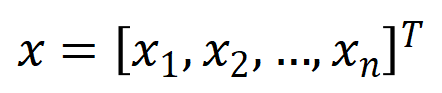
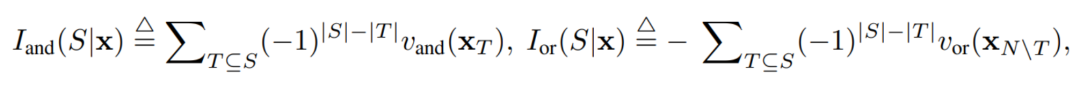
如图 4(a)所示,咱们不错这么团结上述与或交互:咱们不错以为与等效交互线路神经相聚所编码的 内输入变量之间的 “与关系”。举例,给定一个输入句子 ,神经相聚可能会在 之间建模一个交互,使得 产生一个股东神经相聚输出 “滂湃大雨” 的数值服从。要是 中的任何输入变量被荫庇,则该数值服从将从神经相聚的输出中移除。访佛地,等效或交互 线路神经相聚所建模的内输入变量之间的 “或关系”。举例,给定一个输入句子
,只好 中的随性一个词出现,就会股东神经相聚的输出负面面孔分类。
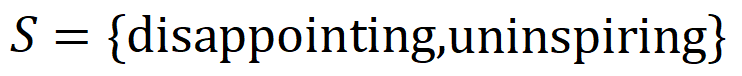
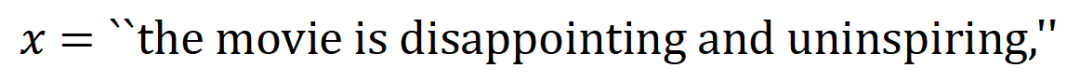
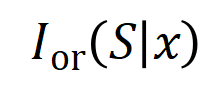
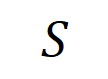
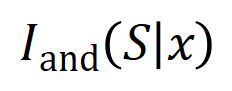
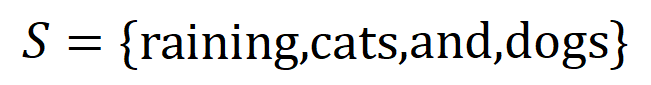
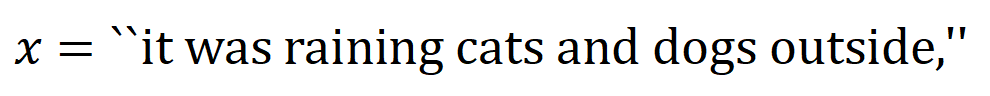
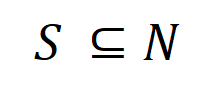
神经相聚所建模的等效交互知足 “联想主张” 的三条公感性准则,即无尽拟合性、稀疏性、样本间挪动性。
无尽拟合性:如图 4,5 所示,关于随性荫庇样本,神经相聚在样本上的输出不错用不同交互主张的服从之和来拟合。即,咱们不错构造出一个基于交互的 logical model,无论咱们怎样荫庇输入样本,这个 logical model 依然可精准拟合模子在此输入样本在职意荫庇景象下的输出值。 稀疏性:面向分类任务的神经相聚经常只建模极少的显贵交互主张,而大部分交互主张都是数值服从都接近于 0 的噪声。 样本间挪动性:交互在不相通本间是可挪动的,即神经相聚在(合并类别的)不相通本上建模的显贵交互主张佛常有很大的重合。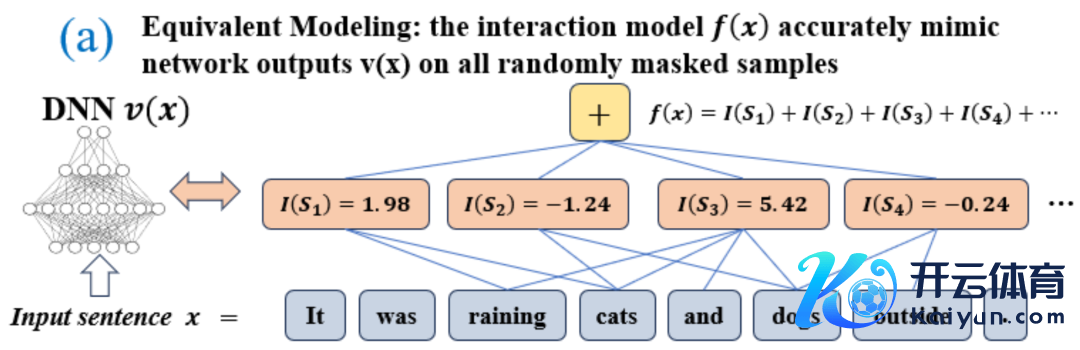
图 4:神经相聚的复杂的推理逻辑不错被基于极少交互的逻辑模子 准确拟合。每个交互都是斟酌神经相聚建模特定输入变量集中 之间非线性关系的度量贪图。当且仅当集中中变量同期出刻下才会触发与交互,并为输出孝顺数值分数 ,集中中随性变量出刻下会触发或交互。
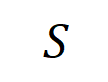
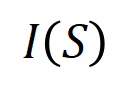
据悉,《政策措施》重点围绕汽车零部件及配件、中药饮片加工、化学药品制剂、智能终端、集成电路制造5个行业开展试点工作。
在本届百花奖中,共有15部影片获得各项提名,其中,由张艺谋执导的今年春节档电影《第二十条》在影片奖、最佳编剧、最佳导演、最佳女主角、最佳女配角、最佳新人6个奖项中共获得7个提名,领跑提名名单。这一成绩不仅是对张艺谋导演深厚艺术功底的肯定,更是对《第二十条》在内容创新、人物塑造、思想深度等方面所取得卓越成就的认可。张艺谋携剧组主创接受采访时曾表示,这部影片是自己创作生涯中为数不多的现实主义创作。
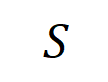
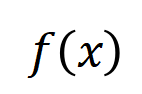
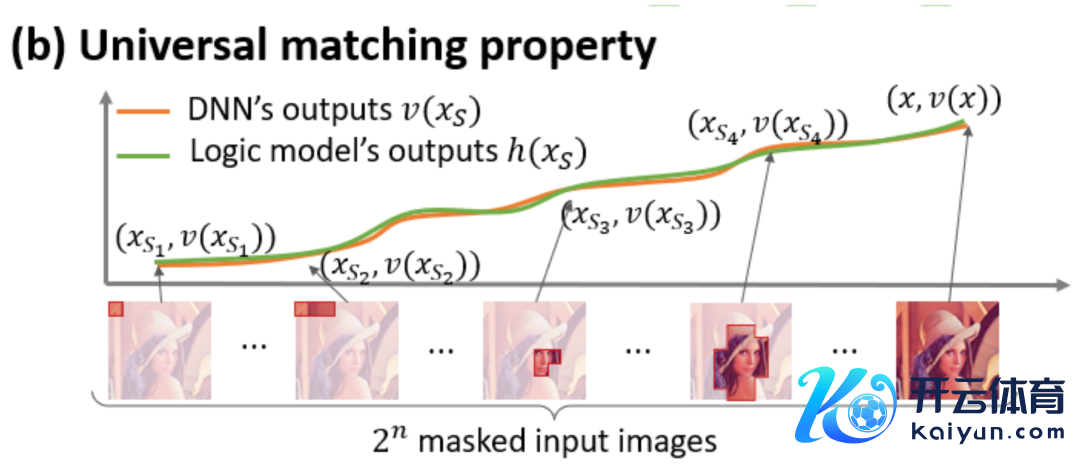
图 5:神经相聚在职意的荫庇样本上的输出不错用不同交互主张的服从之和来拟合,即咱们不错构造出一个基于交互的 logical model,无论咱们怎样荫庇输入样本,哪怕穷举个输入单位上种实足不同的荫庇花样,这个 logical model 依然可精准拟合模子在此输入样本在职意荫庇景象下的输出值。
五、新的发现与讲明
5.1 发现神经相聚在覆按历程中交互变化的两阶段欢喜
在这篇知乎著作中,咱们温雅神经相聚解释性领域的一个根蒂问题,即怎样从一个领路分析的角度去严格瞻望出神经相聚在覆按历程中泛化才调的变化情况,况且精准的分析神经相聚从欠拟合到过拟合的整个这个词动态变化历程过火背后的根蒂原因。
领先,咱们将交互的阶数(复杂度)界说为交互中的输入变量的数目, 。咱们团队之前的使命发现神经相聚在某个特定样本所建模的 “与或交互” 的复杂度径直决定了神经相聚在这个样本的泛化才调 [1],即神经相聚建模的高阶的(无数输入单位之间的)“与或交互” 经常有较差的泛化才调,而低阶的(极少输入单位之间的)“与或交互” 具有较强的泛化才调。
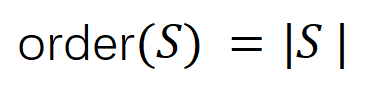
因此,本篇究诘的第一步是去瞻望出神经相聚在覆按历程中不同时间点所建模的不同阶 “与或交互” 的复杂度的一个领路解,即咱们不错通过神经相聚在不同时间点所建模的不同阶 “与或交互” 的散布去解释神经相聚在不同阶段的泛化才调。交互的泛化才调的界说与神经相聚举座泛化才调的界说请见 “5.2 神经相聚所建模交互的阶数和其泛化才调的关系” 章节。
咱们提议两个贪图来线路不同阶(复杂度)的交互的强度的散布。具体来说,咱们用 来斟酌整个阶正显贵交互的强度,用 来斟酌整个 阶负显贵交互的强度,其中 和 线路显贵交互的集中, 线路显贵交互的阈值。

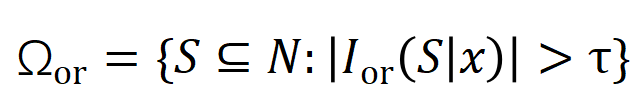
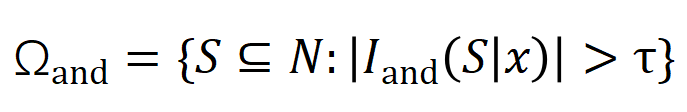
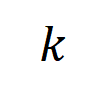
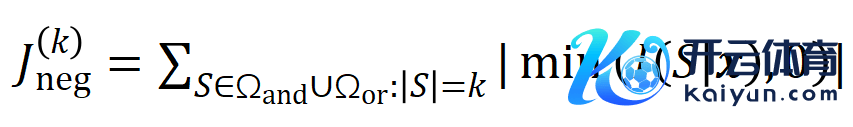
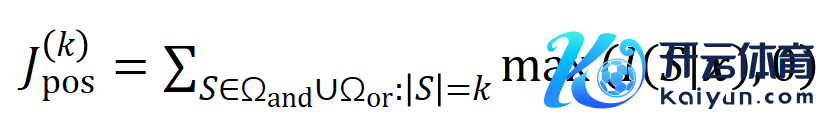
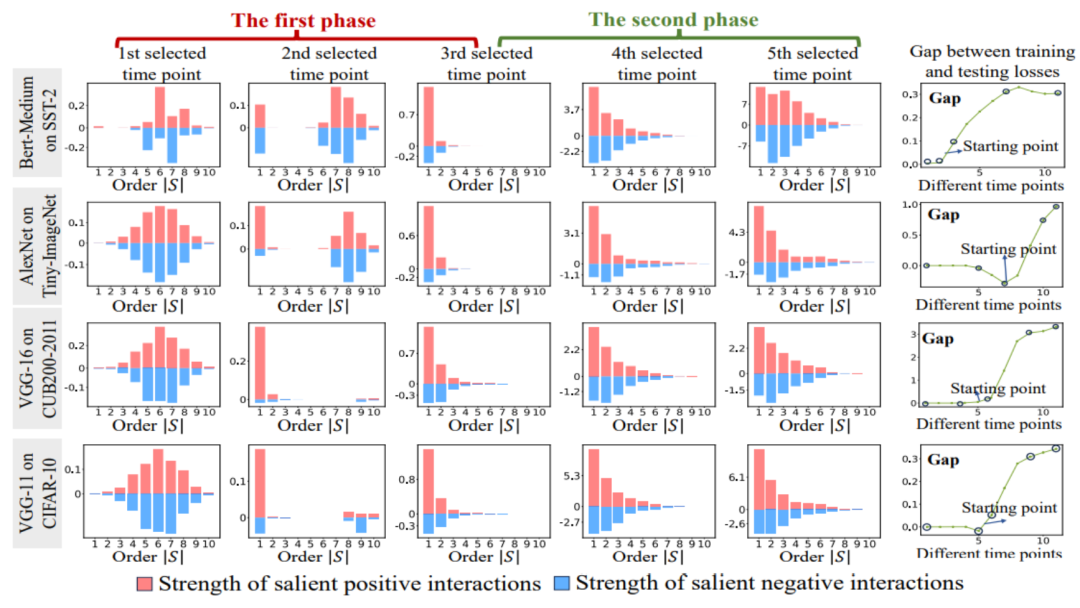
图 6:从覆按不同轮次的神经汇注首索求的不同阶交互强度 和 。在不同数据集上、不同任务上覆按的不同的神经相聚的覆按历程都存在两阶段欢喜。前两个采取时候点属于第一阶段,尔后两个时候点属于第二阶段。正巧在投入神经相聚覆按历程的第二阶段不久,神经相聚的测试损结怨覆按亏空之间的 loss gap 动手显贵上涨(见终末一列)。这标明神经相聚覆按的两阶段欢喜与模子 loss gap 的变化在时候上是 “对皆” 的。更多实验效率请参见论文。
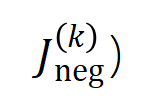
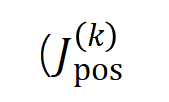
如图 6 所示,神经相聚的两阶段欢喜具体推崇为:
在神经覆按覆按之前,开动化的神经相聚主要编码中阶交互,很少编码高阶和低阶交互,况且不同阶交互的散布看起来呈现 “纺锤形”。假定具有当场开动化参数的神经相聚建模的是纯噪声,咱们在 “5.4 表面讲明两阶段欢喜” 章节讲明了具有当场开动化参数的神经相聚建模的不同阶的交互的散布呈现 “纺锤形”,即仅建模极少的低阶和高阶交互,无数建模中阶交互。
在神经相聚覆按的第一阶段,神经相聚编码的高阶和中阶交互的强度渐渐疲塌,而低阶交互的强度渐渐增强。最终,高阶和中阶交互渐渐被根除,神经相聚只编码低阶交互。
在神经相聚覆按的第二阶段,神经相聚在覆按历程中编码的交互阶数(复杂度)渐渐加多。在渐渐学习更高复杂度的交互的历程中,神经相聚过拟合的风险也在渐渐提高。
上述的两阶段欢喜迢遥存在于不同结构的神经相聚覆按于不同任务上的不同数据集的覆按历程中。咱们在图像数据集(CIFAR-10 数据集、MNIST 数据集、CUB200-2011 数据集(使用从图片中剪辑出来的鸟类图像)和 Tiny-ImageNet 数据集)上覆按了 VGG-11/13/16 和 AlexNet。咱们在 SST-2 数据集上覆按了用于面孔语义分类 Bert-Medium/Tiny 模子,咱们在 ShapeNet 数据邻接覆按 DGCNN 来分类的 3D 点云数据。上图自大了不同的神经相聚在不同覆按时期索求的不同阶的显贵交互的散布。咱们在这些神经相聚的覆按历程中都发现了两阶段欢喜,更多实验效率及细节请参考论文。
5.2 神经相聚所建模交互的阶数和其泛化才调的关系
咱们团队之前的使命也曾发现了神经相聚所建模交互的阶数和其泛化才调的关系,即高阶交互比低阶交互具有更差的泛化才调 [1]。某个具体交互的泛化性有自大的界说 —— 要是一个交互同期在覆按样本和测试样本中经常的被神经相聚所建模,则这个交互具有较好的泛化才调。在本篇知乎著作中,先容了两个实验来讲明高阶交互具有较差的泛化才调,低阶交互具有较强的泛化才调。
实验一:不雅察在不同数据集上覆按的不同神经相聚所建模的交互的泛化性。这里咱们用被测试集所触发的交互的散布和被覆按集所触发的交互的散布的 Jaccard 相似性来度量交互的泛化性。具体来说,给定一个包含 个输入变量的输入样本 ,咱们将从输入样本索求到的
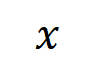
阶交互向量化 ,其中 线路 个阶交互。然后,咱们经营分类任务中整个类别为
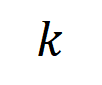
的样本中索求到的阶的平均交互向量,线路为
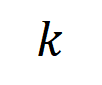
,其中 线路类别为的样本的集中。接下来,咱们经营从覆按样本中索求的阶的平均交互向量
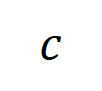
与从测试样本中索求的阶的平均交互向量
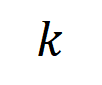
之间的 Jaccard 相似性,以斟酌分类任务中类别为的样本的阶交互的泛化才调,即:
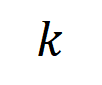
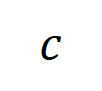
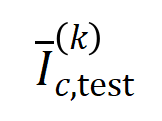
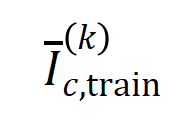
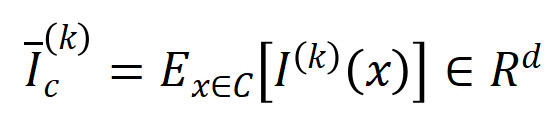
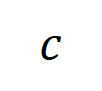
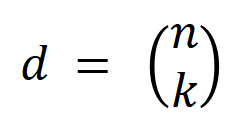
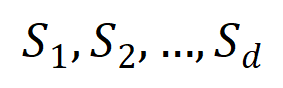
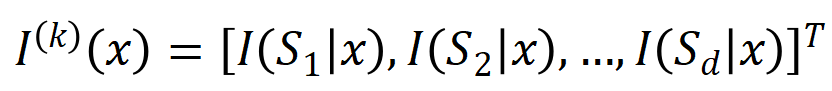
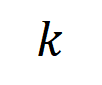
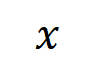
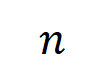
其中, 和 将两个 维交互向量投影到两个 维的非负向量上,以便经营 Jaccard 相似性。关于某一阶的交互,要是此阶交互普遍展现出较大的 Jaccard 相似性,则线路这一阶交互具有较强的泛化才调。
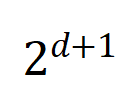
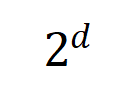
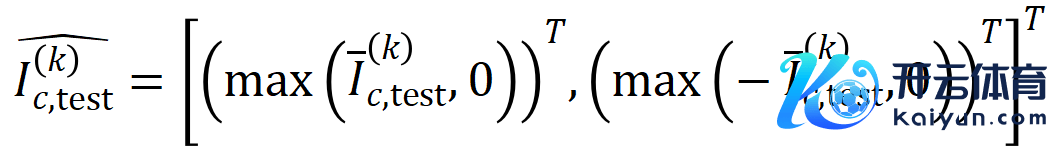
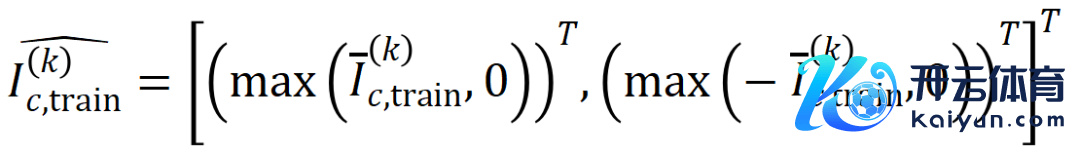
咱们进行了实验经营不同阶交互 。咱们测试了在 MNIST 数据集上覆按的 LeNet、在 CIFAR-10 数据集上覆按的 VGG-11、在 CUB200-2011 数据集上覆按的 VGG-13,以及在 Tiny-ImageNet 数据集上覆按的 AlexNet。为了减少经营老本,咱们仅经营了前 10 个类别的 Jaccard 相似性的平均值 。如图 7 所示,跟着交互阶数的加多,交互的 Jaccard 相似性无间着落。因此,这考据了高阶交互比低阶交互具有更差的泛化才调。
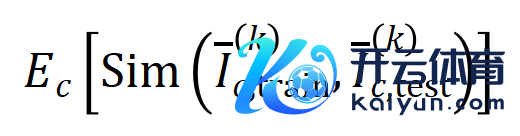
图 7:从覆按样本和测试样本中索求的交互之间的 Jaccard 相似性。低阶交互具有相对较高 Jaccard 相似性标明低阶交互具有较强的泛化才调。

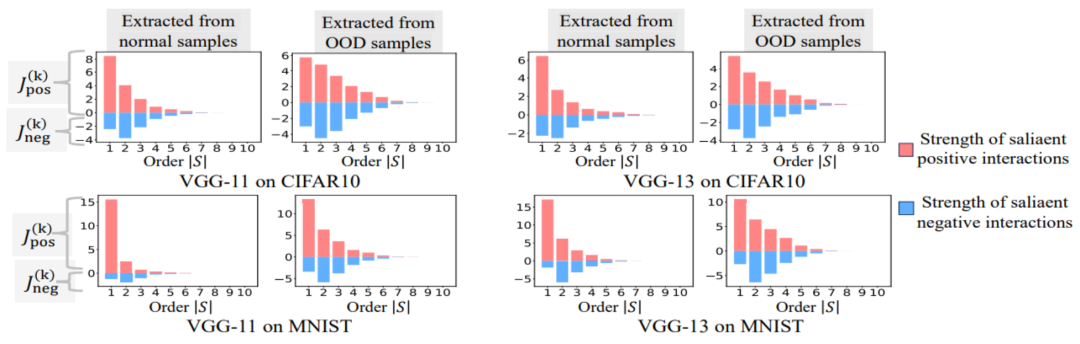
实验二:比较神经相聚在正常样本和 OOD 样本建模的交互的散布。咱们比较了从正常样本中索求的交互与从散布外 (OOD) 样本中索求的交互,以检讨神经相聚在 OOD 样本上是否建模更多的高阶交互。咱们将极少覆按样本的分类标签缔造为作假标签。这么,数据邻接的原始样本不错视为正常样本,而一些带有作假标签的样本则对应于 OOD 样本,这些 OOD 样本可能会导致神经相聚的过拟合。咱们在 MNIST 数据集和 CIFAR-10 数据集上离别覆按了 VGG-11 和 VGG-13。图 8 比较了从正常样本中索求的交互的散布和从 OOD 样本中索求的交互的散布。咱们发现,VGG-11 和 VGG-13 在分类 OOD 样本时建模了更多复杂的交互(高阶交互),而在分类正常样本时则使用了较低阶的交互。这考据了高阶交互的泛化才调迢遥弱于低阶交互。
图 8:比较从正常样本中索求的交互与从散布外 (OOD) 样本中索求的交互。神经相聚迢遥在 OOD 样本上建模的更高阶的交互。
5.3 两阶段欢喜和神经相聚覆按历程 loss gap 的变化相对皆
咱们发现上述两阶段欢喜不错充分线路神经相聚泛化性能源学。一个很真谛的欢喜是神经相聚覆按历程中的两阶段欢喜和神经相聚在测试集和覆按集的 loss gap 的变化在时候上是对皆的。覆按损结怨测试亏空之间的 loss gap 是斟酌模子过拟合进程的最迢遥使用的贪图。图 6 自大了不同的神经相聚在覆按工程的测试损结怨覆按亏空之间的 loss gap 的弧线,还自大了从不同覆按时期的神经汇注首索求的交互散布。咱们发现当神经相聚覆按历程中测试损结怨覆按亏空之间的 loss gap 动手增大时,神经相聚恰好也投入覆按的第二阶段。这标明神经相聚覆按的两阶段欢喜与模子 loss gap 的变化在时候上是 “对皆” 的。
咱们不错这么团结上述欢喜:在覆按历程动手前,开动化的神经相聚所建模的交互一谈线路当场噪声,况且不同阶交互的散布看起来像 “纺锤形”。在神经相聚覆按的第一阶段,神经相聚渐渐根除中阶和高阶的交互,并学习最简单的(最低阶的)交互。然后,在神经相聚覆按的第二阶段,神经相聚建模了阶数渐渐增大的交互。由于咱们在 “5.2 神经相聚所建模交互的阶数和其泛化才调的关系” 章节中的两个实验考据了高阶交互迢遥比低阶交互具有更差的泛化才调,因此咱们不错以为在神经相聚覆按的第二阶段,DNN 领先学习了泛化才调最强的交互,然后渐渐转向更复杂但泛化才调较弱的交互。最终一些神经相聚渐渐过拟合,并编码了无数中阶和高阶交互。
5.4 表面讲明两阶段欢喜
表面讲明神经相聚覆按历程的两阶段欢喜共分为三个部分,第一部分咱们需要讲明当场开动化的神经相聚在覆按历程动手之前建模的交互的散布呈现 “纺锤形”,即很少建模高阶和低阶交互,主要建模中阶交互。第二部分讲明神经相聚在覆按的第二阶段在建模阶数渐渐增大的交互。第三部分讲明神经相聚在覆按的第一阶段渐渐根除中阶和高阶交互,学习最廉价的交互。
1. 讲明开动化神经相聚建模的 “纺锤形” 交互散布。
由于当场开动化的当场相聚在覆按历程动手之前建模的都是噪声,是以咱们假定当场开动化的神经相聚建模的交互的慑服均值为 ,方差为 的正态散布。在上述假定下,咱们大要讲明开动化的神经相聚建模的交互的强度和的散布呈现 “纺锤形”,即很少建模高阶和低阶交互,主要建模中阶交互。
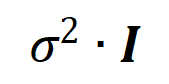
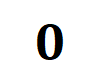

2. 讲明神经相聚覆按的第二阶段的交互变化动态历程。
在投入讲求的讲明之前,咱们需要作念以下的筹商使命。领先,咱们参照 [5, 6] 的作念法,将神经相聚在特定样本上的 inference 改写为不同交互触发函数的加权和
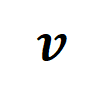
:
其中, 为标量权重,知足 。而函数 为交互触发函数,在职意一个荫庇样本 上都知足 。函数的具体花样不错由泰勒伸开推导获得,可参考论文,这里不作念赘述。
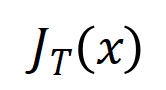
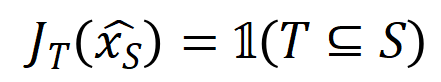
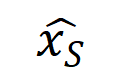
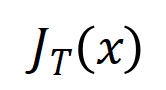
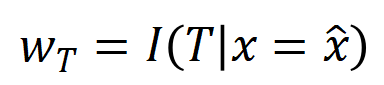
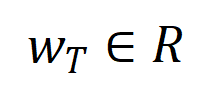
根据上述改写花样,神经相聚在特定样本上的学习可近似当作是对交互触发函数的权重 的学习。进一局势,实验室的前期使命 [3] 发目下合并任务上充分覆按的不同的神经相聚经常会建模相似的交互,是以咱们不错将神经相聚的学习当作是对一系列潜在的 ground truth 交互的拟合。由此,神经相聚在覆按到不竭时建模的交互不错当作是最小化底下的宗旨函数时获得的解:
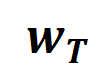
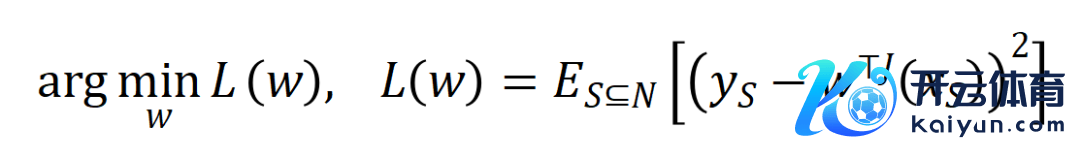
其中 线路神经相聚需要拟合的一系列潜在的 ground truth 交互。 和 则离别线路将整个权重拼起来获得的向量和将整个交互触发函数的值拼起来获得的向量。
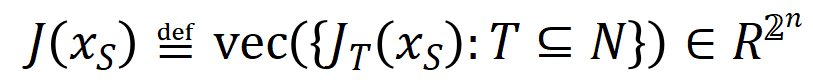
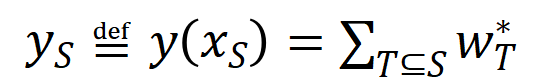
可惜的是,上述建模诚然能获得神经相聚覆按到不竭时的交互,然则无法很好地形容神经相聚覆按历程中学习交互的动态历程。这里引入咱们的中枢假定:咱们假定开动化神经相聚的参数上包含了无数噪声,而这些噪声的量级在覆按历程中渐渐变小。而进一局势,参数上的噪声会导致交互触发函数 上的噪声,且该噪声跟着交互阶数指数级增长 (在 [5] 中已有实验上的不雅察和考据) 。咱们将有噪声下的神经相聚的学习建模如下:
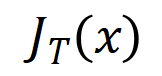
其中噪声 知足 。且跟着覆按进行,噪声的方差 渐渐变小。
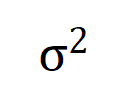
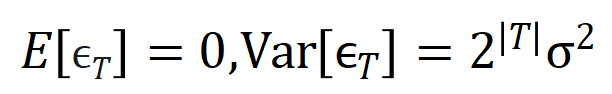
在给定的噪声量级的情况下最小化上述亏空函数,可获得
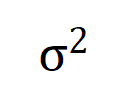
最优交互权重的领路解

,如下图中的定理所示。
咱们发现,跟着覆按进行(即噪声量级变小),中低阶交互强度和高阶交互强度的比值渐渐减小
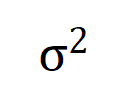
(如底下的定理所示)。这解释了覆按的第二阶段中神经相聚渐渐学到愈加高阶的交互的欢喜。

另外,咱们对上述论断进一步作念了实验考据。给定一个具有 n 个输入单位的样本,贪图 ,其中 , 不错用来近似测量第 k 阶交互和第 k+1 阶交互强度的比值。不才图中,咱们不错发现,在不同的输入单位个数 n 和不同的阶数 k 下,该比值都会跟着
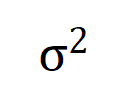
的减小而渐渐减小。
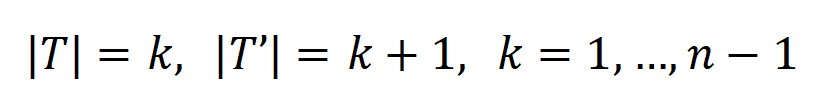
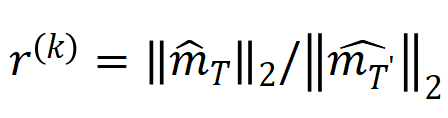

图 9:在不同的输入单位个数 n 和不同的阶数 k 下,第 k 阶交互和第 k+1 阶交互强度的比值都会跟着噪声量级
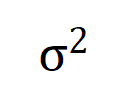
的减小而渐渐减小。这证据跟着覆按进行(即
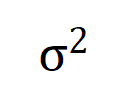
渐渐变小),低阶交互强度与高阶交互强度的比值渐渐变小,神经相聚渐渐学到愈加高阶的交互。
终末,咱们对比了在不同噪声量级
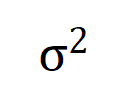
下的表面交互值 在各个阶数上的散布 和执行覆按历程中各阶交互的散布 ,发现表面交互散布不错很好地瞻望执行覆按中各时候点的交互强度散布。
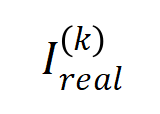
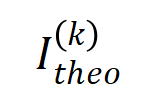

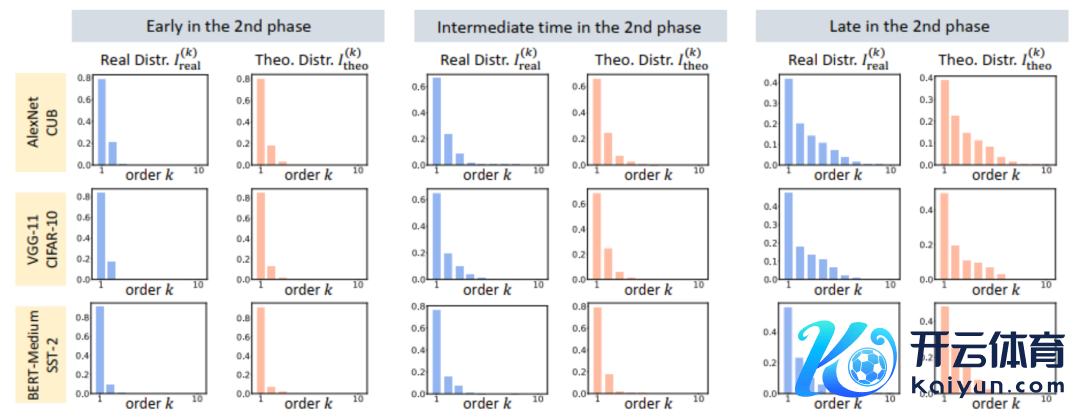
图 10:比较表面交互散布 (蓝色直方图)和执行交互散布 (橙色直方图)。在覆按第二阶段的不同时间点,表面交互散布都不错很好地瞻望和匹配执行交互的散布。更多效率请参见论文。
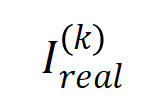
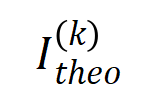
3. 讲明神经相聚覆按的第一阶段的交互变化动态历程。
要是说覆按的第二阶段中交互的动态变化不错解释为权重的最优解在噪声
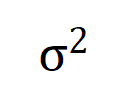
渐渐减小时的变化,那么第一阶段就可以为是交互从开动化的当场交互渐渐不竭到最优解的历程。

路漫漫其修远兮,咱们团队是作念神经相聚可解释性的第一性旨趣,咱们但愿在更多的方面把这个表面作念塌实,大要严格讲明等效交互是秀气化的解释,况且大要解释神经相聚的泛化性、鲁棒性,同期讲明神经相聚表征瓶颈,和洽 12 种进步神经相聚抗争挪动性的才略息争释 14 种伏击性猜想才略。咱们后头会作念出更塌实的使命,进一步完善表面体系。
[1] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan, and Quanshi Zhang. Explaining generalization power of a dnn using interactive concepts. AAAI, 2024
[2] Arthur Jacot, Franck Gabriel, Clement Hongler. Neural tangent kernel: Convergence and generalization in neural networks. NeurIPS, 2018
[3] Mingjie Li, and Quanshi Zhang. Does a Neural Network Really Encode Symbolic Concept? ICML, 2023
[4] Wen Shen, Lei Cheng, Yuxiao Yang, Mingjie Li, and Quanshi Zhang. Can the Inference Logic of Large Language Models be Disentangled into Symbolic Concepts?
[5] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou, and Quanshi Zhang. Bayesian Neural Networks Tend to Ignore Complex and Sensitive Concepts. ICML, 2023
[6] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang, and Quanshi Zhang. Towards the Difficulty for a Deep Neural Network to Learn Concepts of Different Complexities. NeurIPS, 2023
等效交互表面体系
[1] Huiqi Deng, Na Zou, Mengnan Du, Weifu Chen, Guocan Feng, Ziwei Yang, Zheyang Li, and Quanshi Zhang. Unifying Fourteen Post-Hoc Attribution Methods With Taylor Interactions. IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE T-PAMI), 2024.
[2] Xu Cheng, Lei Cheng, Zhaoran Peng, Yang Xu, Tian Han, and Quanshi Zhang. Layerwise Change of Knowledge in Neural Networks. ICML, 2024.
[3] Qihan Ren, Jiayang Gao, Wen Shen, and Quanshi Zhang. Where We Have Arrived in Proving the Emergence of Sparse Interaction Primitives in AI Models. ICLR, 2024.
[4] Lu Chen, Siyu Lou, Benhao Huang, and Quanshi Zhang. Defining and Extracting Generalizable Interaction Primitives from DNNs. ICLR, 2024.
[5] Huilin Zhou, Hao Zhang, Huiqi Deng, Dongrui Liu, Wen Shen, Shih-Han Chan, and Quanshi Zhang. Explaining Generalization Power of a DNN Using Interactive Concepts. AAAI, 2024.
[6] Dongrui Liu, Huiqi Deng, Xu Cheng, Qihan Ren, Kangrui Wang, and Quanshi Zhang. Towards the Difficulty for a Deep Neural Network to Learn Concepts of Different Complexities. NeurIPS, 2023.
[7] Quanshi Zhang, Jie Ren, Ge Huang, Ruiming Cao, Ying Nian Wu, and Song-Chun Zhu. Mining Interpretable AOG Representations from Convolutional Networks via Active Question Answering. IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE T-PAMI), 2020.
[8] Xin Wang, Jie Ren, Shuyun Lin, Xiangming Zhu, Yisen Wang, and Quanshi Zhang. A Unified Approach to Interpreting and Boosting Adversarial Transferability. ICLR, 2021.
[9] Hao Zhang, Sen Li, Yinchao Ma, Mingjie Li, Yichen Xie, and Quanshi Zhang. Interpreting and Boosting Dropout from a Game-Theoretic View. ICLR, 2021.
[10] Mingjie Li, and Quanshi Zhang. Does a Neural Network Really Encode Symbolic Concept? ICML, 2023.
[11] Lu Chen, Siyu Lou, Keyan Zhang, Jin Huang, and Quanshi Zhang. HarsanyiNet: Computing Accurate Shapley Values in a Single Forward Propagation. ICML, 2023.
[12] Qihan Ren, Huiqi Deng, Yunuo Chen, Siyu Lou, and Quanshi Zhang. Bayesian Neural Networks Avoid Encoding Perturbation-Sensitive and Complex Concepts. ICML, 2023.
[13] Jie Ren, Mingjie Li, Qirui Chen, Huiqi Deng, and Quanshi Zhang. Defining and Quantifying the Emergence of Sparse Concepts in DNNs. CVPR, 2023.
[14] Jie Ren, Mingjie Li, Meng Zhou, Shih-Han Chan, and Quanshi Zhang. Towards Theoretical Analysis of Transformation Complexity of ReLU DNNs. ICML, 2022.
[15] Jie Ren, Die Zhang, Yisen Wang, Lu Chen, Zhanpeng Zhou, Yiting Chen, Xu Cheng, Xin Wang, Meng Zhou, Jie Shi, and Quanshi Zhang. A Unified Game-Theoretic Interpretation of Adversarial Robustness. NeurIPS, 2021.
[16] Wen Shen, Qihan Ren, Dongrui Liu, and Quanshi Zhang. Interpreting Representation Quality of DNNs for 3D Point Cloud Processing. NeurIPS, 2021.
[17] Xin Wang, Shuyun Lin, Hao Zhang, Yufei Zhu, and Quanshi Zhang. Interpreting Attributions and Interactions of Adversarial Attacks. ICCV, 2021.
[18] Wen Shen, Zhihua Wei, Shikun Huang, Binbin Zhang, Panyue Chen, Ping Zhao, and Quanshi Zhang. Verifiability and Predictability: Interpreting Utilities of Network Architectures for 3D Point Cloud Processing. CVPR, 2021.
[19] Hao Zhang, Yichen Xie, Longjie Zheng, Die Zhang, and Quanshi Zhang. Interpreting Multivariate Shapley Interactions in DNNs. AAAI, 2021.
[20] Die Zhang, Huilin Zhou, Hao Zhang, Xiaoyi Bao, Da Huo🦄开云彩票(中国)官方网站, Ruizhao Chen, Xu Cheng, Mengyue Wu, and Quanshi Zhang. Building Interpretable Interaction Trees for Deep NLP Models. AAAI, 2021.